Gt Ga Notes Ra

Posted Oct 10, 2024 Updated Oct 20, 2024

By yxlow

19 min read

Modular Arithmetic (RA1)

Short overview of topics:

Math primer
- modular Arithmetic
- multiplicative inverses
- Euclid’s GCD algorithm
Fermat’s little theorem
- RSA algorithm
Primality testing
- is a number a prime number? or a composite number
- Generate random prime numbers

Huge integers

For huge n, consider n-bit integers, x,y, N, in the order of 1024 or even 2048 bits.

Modular Arithmetic

For integer x, x mod 2 = least significant bit of x, which tells you if x is even or odd. We can also do this by x/2 and get the remainder.

For integer $N \geq 1: x mod N$ is the remainder of x when divided by N.

Some additional notation:

\[X \equiv Y \bmod N\]

means $\frac{X}{N}, \frac{Y}{N}$ have same remainder, another way of writing this is:

\[x \bmod N = r \iff x = qN + r, q,r \in \mathbb{Z}\]

Then we have the following:

if $x \equiv y \bmod N $ and $a \equiv b \bmod N$ then $x+a \equiv y+b \bmod N$ and $xa \equiv yb \bmod N$

Modular Exponentiation

n-bit numbers, compute $x^y \bmod N$.

Consider the simple algorithm:

\[\begin{aligned} x \bmod N &= a_1 \\ x^2 \equiv a_1x \bmod N &= a_2 \\ \vdots \\ x^y = a_{y-1}x \bmod N &= a_n \end{aligned}\]

Multiplying two n-bit numbers and dividing by a n-bit number takes $O(n^2)$ per round, since we have y rounds where $y \leq 2^n$, the overall time complexity is $O(n^2 2^n)$ which is horrible

\[\begin{aligned} x \bmod N &= a_1 \\ x^2 \equiv (a_1)^2 \bmod N &= a_2 \\ x^4 \equiv (a_2)^2 \bmod N &= a_4 \\ x^8 \equiv (a_4)^2 \bmod N &= a_8 \\ \vdots \\ \end{aligned}\]

Then we can look at the binary representation of $y$ and find the appropriate $a_i$. For example if $y=25 = 11001$, then we need $a_{2^4=16} \ast a_{a^3 = 8} \ast a_{2^0=1} = a_{25}$

Mod-Exp algorithm

Note that for even $y$, $x^y = (x^{y/2})^2$, and for odd $y$, $x^y = x(x^{\lfloor y/2 \rfloor})^2$

mod-exp(x,y,N)
  Input: n-bit integers, x,y N >= 0
  Output: pow(x,y) mod N
  if y = 0, return(1)
  z = mod-exp(x, floor(y/2), N)
  if y is even:
    return (z^2 mod N)
  else:
    return (xz^2 mod N)

Multiplicative inverses

x is the multiplicative inverse of $z \bmod N$ if $xz \equiv 1 \bmod N$, which can be re-written as :

\[x \equiv z^{-1} \bmod N\]

Note that the $z$ is also the inverse of x, i.e $z \equiv x^{-1} \bmod N$

Note that the inverse is not guaranteed to exists, consider $N=14$, what is the inverse of $4 \mod 14$?

Inverse: Existence

The key idea here is if $x,N$ shares a common divisor, then it has no inverse.

Theorem: $x^{-1} \bmod N$ exists if and only if $gcd(x,N)=1$, gcd stands for greatest common divisor. This also means x and N are relatively prime.

In addition, if we always report $x^{-1} \bmod N$ in $0,1,…,N-1$ if it exists, it is unique and does not exists otherwise. For instance, $3^{-1} \equiv 4 \bmod 11$, but so is $15,26,-7$. Etc $3*-7 = -21 \bmod 11 = -1 $

Proof. Lets suppose $x^{-1} \bmod N$ has two inverses, $y \equiv x^{-1} \bmod N, z \equiv x^{-1} \bmod N, y\cancel{\equiv} z, 0 \leq y \neq z \leq N-1$.

This implies that $xy \equiv xz \equiv 1 \bmod N$. But if we multiply each by $x^{-1}$, then $x^{-1}xy \equiv x^{-1}xz \bmod N$ which implies $y \equiv z \bmod N$ which is a contradiction.

Inverse: Non existence

if $gcd(x,N) > 1$ then $x^{-1} \equiv \bmod N$ does not exists.

Lets assume $z = x^{-1} \bmod N \implies xz \equiv 1 \bmod N$ and $x,z$ shares a common divisor, $k > 1$.

This means that $xz = gN+1$, which means $akz = g(bk)+1$, for some $a$ and $b$ since $x,N$ share some common divisor $k$. But this implies that $k(az-gb) = 1$, then $az-gb = \frac{1}{k}$ which shows that $az-gb$ is a fraction but $az-gb$ is an integer since a,z,g,b are integers and $k >1$, which is a contradiction.

Euclid Rule

For integers x,y where $ x \geq y > 0$:

\[gcd(x,y) = gcd(x \bmod y ,y)\]

Proof: $gcd(x,y) = gcd(x-y,y)$, and if this is true we take x and minus y from it until we are no longer able to do so. This gives us exactly $x \bmod y$.

Now, to proof $gcd(x,y) = gcd(x-y,y)$:

if $d$ divides $x,y$ then $d$ divides $x-y$
if $d$ divides $x-y, y$, then it divides $x$ since we can just sum them up.

Euclid’s GCD algorithm

Euclid(x,y):
  input: integers (x,y) where x >= y >= 0
  output: gcd(x,y)

  if y = 0:
    return(x)
  else:
    return (Euclid(y, x mod y))

In the base case we are looking at y = 0, which is $gcd(x,0)$ What are the divisors of zero? How should we define this? What is a reasonable manner of defining the divisors of zero? Well, we got to this case by taking the GCD of sum multiple $x$ with $x$:

\[gcd(x,0) = gcd(kx, x) = x\]

Before we analyize the runtime analysis, lets prove:

Lemma: if $x \geq y$ then $x \bmod y < \frac{x}{2}$.

If $y \leq x/2$ then $x \bmod y \leq y-1 < y \leq x/2$
If $y > x/2, \lfloor \frac{x}{y}\rfloor =1$ then $x \bmod y = x-y < x - \frac{x}{2} \leq \frac{x}{2}$

Note, because of the lemma, each rounds the values decreasings by half:

\[(x,y) \rightarrow (y, x\bmod y) \rightarrow (\underbrace{x \bmod y}_{< \frac{x}{2}}, y\bmod x \bmod y ) \\ \implies 2n \text{ rounds}\]

So there is a total of $2n$ rounds. We can now do our run-time analysis.

Runtime analysis:

x mod y takes $O(N^2)$ time to compute where $N$ is the number of bits, and this is for a single round.
Total of $2n$ rounds
Total of $O(n^3)$ runtime.

Extended Euclid Algorithm

This is to compute the inverse of $x \bmod y$. Suppose $d = gcd(x,y)$ and we can express $d=x\alpha+y\beta$ and we have the following:

\[d = gcd(x,y) = d=x\alpha+y\beta\]

if $gcd(x,N) =1$ then $x^{-1} \bmod N$ exists and we have the following:

\[\begin{aligned} d = 1 &= x\alpha + N\beta \\ 1 &\equiv x\alpha + \underbrace{N\beta}_{0} \bmod N \\ x^{-1} &\equiv \alpha \bmod N \end{aligned}\]

Similarly,

\[\beta = N^{-1} \bmod X\]

Ext-Euclid(x,y)
  input: integers, x,y where x >= y >= 0
  output: integers d, α,β where d = gcd(x,y) and d = xα+yβ

  # remember gcd(x,0) = x, so we just set α = 1,β = 0
  if y = 0:
    return (x,1,0)
  else:
    d,α',β' = Ext-Euclid(y, x mod y)
    return (d, β', α' - floor(x/y)β')

The proof of the final expression can be found in the textbook, enjoy!

Runtime analysis:

Similarly, $O(n^2)$ to compute $x \bmod y$ and calculating $\lfloor \frac{x}{y} \rfloor$
$n$ rounds
Total of $O(n^3)$

Summary:

Fast Modular Exponentiation algorithm
How to calculate multiplicative inverse
- Euclid’s GCD algorithm - $gcd(x,y)$
- Extended Euclid’s algorithm to compute $x^{-1} \bmod N$

RSA (RA2)

Fermat’s little theorem

If p is prime then for every $1 \leq z \leq p-1$, so $gcd(z,p) = 1$ then:

\[z^{p-1} \equiv 1 \bmod p\]

This is the basis of RSA algorithm and also allows us to test if a number $x$ is prime.

Proof: Let $S = {1,2,3,…,p-1}, S’ = zS \bmod P = { i \times z \bmod p, i = 1, …, p-1}$.

For example $p=7,z=4, S={1,2,…,6}, S’ = {4,1,5,2,5,6}$. Notice that the sets are the same, just in different order, and we are going to use $S=S’$ to prove Fermat’s little theorem.

To proof that $S=S’$, we need to show elements of $S’$ are distinct and non zero, which implies $\lvert S’ \lvert = p-1$.

Part one - show that elements of $S’$ are distinct and we do this by contradiction, suppose for some $i \neq j$:

\[iz \equiv jz \bmod P\]

And since $P$ is a prime number, we know then that every element in $S$ has an inverse mod $P$, so $z$ is an element in S since $z$ is between a number $1, P-1$. Recall that: $P$ is prime $\implies z^{-1} \bmod p$ exists, multiplying both sides by $z^{-1}$

\[\begin{aligned} izz^{-1} &\equiv jzz^{-1} \bmod P \\ i &\equiv j \bmod P \end{aligned}\]

which is a contradiction.

Part two - Show that they are non zero. Suppose we have an index $i$ such that:

\[iz \equiv 0 \bmod P\]

and since $z^{-1}$ exists,

\[\begin{aligned} izz^{-1} &\equiv 0z^{-1} \bmod P \\ i &\equiv 0 \bmod P \end{aligned}\]

which is also a contradiction since $i$ is between $1, P-1$.

Back to the proof of Fermat’s little theorem, is to show that $z^{p-1} \equiv \bmod P$ if $P$ is prime. We have $S=S’$, then:

\[\begin{aligned} \prod_{i=1}^{P-1} i &\equiv \prod_{i=1}^{P-1} i \times z \bmod P\\ (P-1)! & \equiv z^{P-1} (P-1)! \bmod P \\ \text{Since } 1^{-1}, 2^{-1}, 3^{-1},...,&(P-1)^{-1} \text{ exists:} \\ \cancel{(P-1)!} & \equiv z^{P-1} \cancel{(P-1)!} \bmod P \\ 1 &\equiv z^{P-1} \bmod P \end{aligned}\]

Euler’s theorem

Euler theorem is the generalization of Fermat’s little theorem

For any $N,z$ where $gcd(z,N) =1$ then:

\[z^{\phi(N)} \equiv 1 \bmod N\]

where $\phi(N)$ is the number of integers between 1 and $N$ which are relatively prime to $N$, i.e the size of the set - $\lvert { x: 1\leq x \leq N, gcd(x,N) = 1} \lvert$.

$\phi$ is also known as Euler’s totient function
when $P$ is prime, then there is $P-1$ numbers relatively prime to $P$. So, $\phi(P) = P-1$.

So, for primes $p,g$ where $N=pq$, this implies that $\phi(N) = (p-1)(q-1)$

Consider $N=pq$ as $1p, 2p, … , qp$ so there are $q$ multiples of $p$.
Likewise, $q, 2q, …, pq$ there are $p$ multiples of $q$.
So, we need to exclude all these numbers!
Therefore we get $pq - p - q + 1$ which equals to $(p-1)(q-1)$
- The $+1$ comes from $pq = pq$ which is a duplicate so we need to add 1 back.

With this, we can re-write Euler theorem as the following:

\[z^{(p-1)(q-1)} \equiv 1 \bmod pq\]

And this is going to allow us to use $p-1,q-1$ to generate a encryption and decryption key.

RSA Idea

Fermat’s Theorem:

For prime $P$, take $b,c$ where $bc \equiv \bmod P-1$. This means we can re-write $bc = 1+ k(P-1)$ for some integer $k$. We then take a number $Z$ between $1$ and $P-1$:

\[\begin{aligned} z^{bc} &\equiv z^{1+K(P-1)} \bmod P \\ &\equiv z (\underbrace{z^{(P-1)}}_{1 \text{by Fermat's }})^k \bmod P \\ &\equiv z \bmod P \end{aligned}\]

The problem here is I need to tell everyone $P$, and given $b$, they are able to figure out $c$ which is the inverse of $b$ with respect to $\bmod P-1$.

Euler’s theorem:

Take $d,e$ where $de \equiv 1 \bmod (p-1)(q-1)$, and $N = pq$:

\[\begin{aligned} z^{de} &\equiv z \times (\underbrace{z^{(p-1(q-1))}}_{1})^k \bmod N \\ &\equiv z \bmod N \end{aligned}\]

Note the terms $D$ and $E$ decryption, encryption. So given a message $Z$, tell the other party $E$ and $N$:

If the other party wants to send you the message $Z$
- raise it to the power of $E$ and get $\bmod N$, i.e $z^E \bmod N$
- send it over
On my end, I compute $D$, which is the inverse of $D = E^{-1} \bmod (q-1)(p-1)$ which is my decryption key
Take the encrypted message $z^E \bmod N$, raise to the power $D$ to get $z^{DE} \bmod N$ which gives me $Z$, the original message.

Notice that the other party only knows $N$, is it possible for the other party to figure out $(p-1)$ or $(q-1)$?

Even if you tell the other party $pq$, the other party is also unable to get $(p-1)$ or $(q-1)$
But I can compute $D$ since I know $p,q$ and $E$.

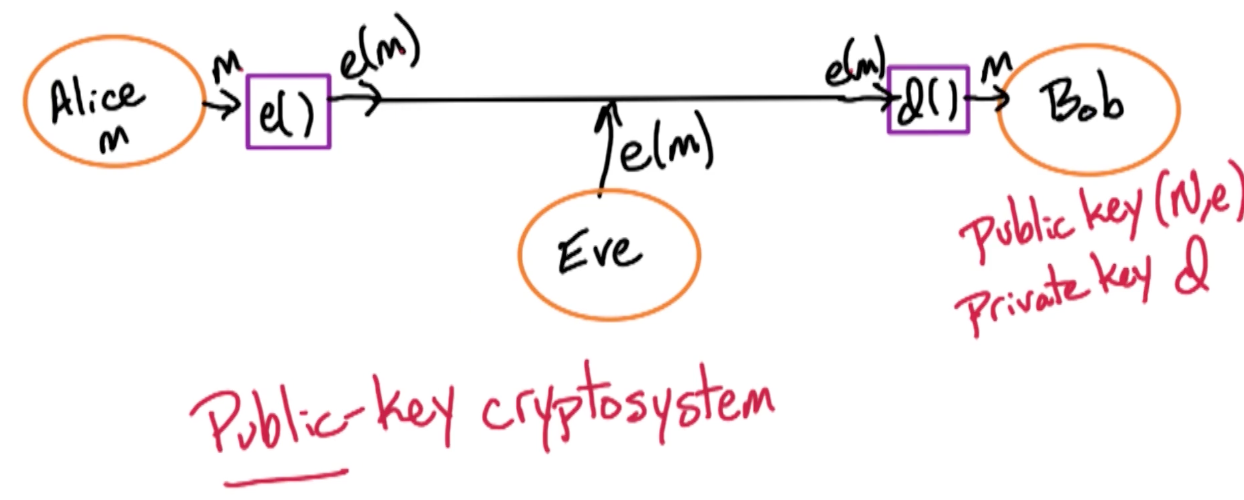
Here is an image to illustrate:

Bob

Bob picks $2$ n-bit random primes $p, q$
Bob chooses $e$ relatively prime to $(p-1)(q-1)$
- Let $N=pq$ and try $e=3,5,7,11…$
- Good to keep encryption key small, easier for someone to encrypt information and send it to you.
- If you are unable to do so, usually you go back to the previous step
Bob publishes his public key $(N,e)$
Bob computes his private key
- $d \equiv e^{-1} \bmod (p-1)(q-1)$
- We can do this because of the extended Euclid algorithm.

Alice

Looks up Bob’s public key $(N,e)$
Computes $y \equiv m^e \bmod N$
- Using the fast mod-exp algorithm
Sends $y$ to bob

Bob

Bob receives $y$
Decrypts by computing $y^d \bmod N=m$
- This is because $y = m^{ed} \bmod N$
- $m^{ed} = m^{1+k(p-1)(q-1)} \bmod N$
- $m^{1+k(p-1)(q-1)} \bmod N = m \bmod N$
  - This is because of euler theorem
- This also holds when $M,N$ has a common factor namely $P$ or $Q$
  - You can still prove this statement holds with the chinese remainder theorem

Now, the question is, how do we generate this random prime number to start with?

RSA Pitfalls

Attack number one When $gcd(m,N) >1$, and $gcd(m,N) = p, N=pq$

$(m^e)^d \equiv \bmod N $ by the chinese remainder theorem
$y \equiv m^e \bmod N$
If $P$ divides $m, N$ since $gcd(m,N) = p$
- Then it is also going to divide $y$
- This means that $gcd(y,N) = p$
- The attacker can then reverse engineer $q$

Attack number two when $gcd(m,N) > 1$ and $m$ not too large, $m < N$ but $m < 2^n, N \geq 2^n$

But in this case, we $m$ cannot be too small, for example if $e=3$, then $m^3 < N$, we simply have $y = m^3$ since $\bmod N$ does nothing! To reverse the message we can simply just take the cube root.

To avoid this we can choose a random number $r$, $m\oplus r$ or $m+r$, and we can send the padded message, as well as a second message that is r itself.
- As long as r is not too small, you will be fine.
- Imagine you’re the receiving user, you receive $m+r$ and $r$, you can then reverse engineer it to get $m$

Attack number three

Send the same $m$ for $e$ times, then we have $(N_1,3), (N_2,3), (N_3,3)$.

Then we have $Y_i, \equiv m^3 \bmod N_i$ and they can figure out $m$ by using the chinese remainder theorem. (DPV 1.44)

RSA Algorithm

Choose primes $p,g$ let $N=pg$
Find $e$ where $gcd(e,(p-1)(q-1))=1$
- This means we want $e$ that is relatively prime to $(p-1)(q-1)$
- This means $e$ has an inverse by Fermat’s little theorem.
Let $d \equiv e^{-1} \bmod (p-1)(q-1)$
- Use the extended Euclid algorithm
- Keep this private key $d$ secret
Publish public key $(N,e)$
Given a message $m$, Encrypt $m$ by $y \equiv m^e \bmod N$
- Send over message $y$
Decrypt $y$ by $y^d \bmod N = m$

Why RSA is hard to break - the whole world knows $N=pq$ but only we know $(p-1)(q-1)$, and therefore only we can compute the inverse of $e^{-1} \bmod (p-1)(q-1)$

A natural question is, can you get $(p-1)(q-1)$ from $N$ without knowing $p$ and $q$ individually?
The assumption is no, it is not possible to do that. The only way to get $p-1,q-1$ is to factor $N$ into $p$ and $q$.

Random primes

let r be a random n-bit number

Choose random r 
  check if r is prime
    if yes:
      output r
    else:
      try again

A random number can be chosen by a n-bit strings.

Runtime:

Primes are dense, $Pr(\text{r is prime}) \approx \frac{1}{n}$, so you can expect to have a random prime number after $n$ tries, so, complexity here is $O(n)$.

Primality: Fermat’s test

Recall that if $r$ is prime then for all $z \in {1,. ..,r-1}$, $z^{r-1} \equiv 1\bmod r$.

So, we need to find $z$ where $z^{r-1} \cancel{\equiv} 1 \bmod r \implies r$ is composite. We call this $z$ a Fermat witness with respect to Fermat’s little theorem.

Does every composite $r$ have a Fermat witness?
- Surprisingly, YES!
How do we find one?
- In fact every composite number has multiple Fermat witness
- Some exceptions such as Pseudo Primes

Fermat Witnesses

Fermat witness for $r : z \text{ if } 1 \leq z \leq r-1 \text{ & } z^{r-1} \cancel{\equiv} 1 \bmod r$, then the number $r$ is composite.

First proof that every composite $r$ has $\geq 1$ Fermat witness. Since $r$ is composite, there is at least two divisors.

Take $z$ where $gcd(r,z) = z$ since $z \leq r-1$, and since $r$ is composite, we know this divisor is greater than one so $z > 1$. So any $z$ which is not relatively prime to $r$ and $r$ is composite will work.

This implies that $z^{-1} \bmod r$ does not exists because it only exists if and only if the $gcd(r,z) = 1$ and this is also from the inverse existence.

Suppose $z^{r-1} \equiv 1 \bmod r$, then we have $z^{r-2} \times z \equiv 1 \bmod r$, so $z^{-1} \equiv z^{r-2} \bmod r$ which is a contradiction.

Feel free to see Dpv 1.3 for more information.

Trivial Fermat witness : $z$ where $gcd(z,r) > 1$
Non-trivial Fermat witness is where $gcd(z,r) = 1$
- Some composite numbers have no non-trivial fermat witnesses, these are called pseudo primes, but those are relatively rare.
- For all other composite numbers, they have at least one non-trivial Fermat witness, and if they have at least one, they in fact have many Fermat witnesses.
- Therefore, it will be easy to find a Fermat witness
Trivial Fermat witnesses always exists!
- Every composite number has at least two trivial Fermat witnesses!
- They are dense and therefore easy to find

Non-Trivial Witnesses

$z$ is a nontrivial Fermat witness for $f$ if $z^{r-1} \cancel{\equiv} 1 \bmod r$ and $gcd(z,r)=1$.

Carmichael numbers - sort of pseudoprime numbers
- They behave like primes with respect to Fermat’s little theorem
A Carmichael number is a composite number $r$ with NO nontrivial Fermat witnesses
Such a number is going to be inefficient to use Fermat’s test to prove that $r$ is a composite number
- Find a different way to deal with them
These Carmichael numbers are rare
- smallest one are 561 and 1105, 1729 and so on
- Ignore them for now

Lemma: if $r$ has $\geq 1$ non trivial Fermat witness, then $\geq \frac{1}{2}$ that $z \in {1,2,..,r-1}$ are Fermat witness.

Proof is in the book, enjoy yourself as usual!
Question still remains, how to check a number is prime?
- Take $z$ from the set ${1,2,..,r-1}$ and raise it to the power $r-1$ and look at $\bmod r$ and see whether it is one or not.

Simple Primality tests

For n-bit r

choose z randomly from {1,2,...,r-1}
Compute pow(z, r-1) === 1 mod r
if pow(z, r-1) === 1 mod r:
  then output r is prime 
else
  output r is composite (z is a witness to the fact that r is composite)

For prime $r$, $z^{r-1} \equiv 1 \bmod r$ is true because of Fermat’s little theorem.

So Pr(algorithm outputs $r$ is prime) = 1

For composite $r$ and assume that it is not a carmichael number. Sometimes the algorithm is going to be correct, it is going to output that $r$ is composite. This happens when it finds a $z$ which is a Fermat witness. $z^{r-1} \cancel{\equiv} 1 \bmod r$

sometimes it is going to get confused, it is going to make a mistake, and it is going to find a $z$ which $z^{r-1} \equiv 1 \bmod r$, so it is going to think that $r$ is prime.
Recall that at most half of them are not witnesses
The Pr(algorithm outputs $r$ is prime) $\leq \frac{1}{2}$

The question now is, can we improve this error probability of a false positive of $\frac{1}{2}$

Better primality test

Instead of choosing a particular $z$, we choose $k-z$ and run the algorithm k times.

Then Pr(algorithm outputs $r$ is prime) $\leq (\frac{1}{2})^k$. You can think of it as a coin toss each with probability $\frac{1}{2}$. So the probability that the coin toss is all tails with k flips is $(\frac{1}{2})^k$.

So you can take $k=100$, so $(\frac{1}{2})^{100}$ is a very small number and you will be willing to take the risk on that.

Again we assume that the numbers are not Carmichael
to deal with these Carmichael, it is not that much more complicated of an algorithm

Dealing with Carmichael

So we know it is composite if there is a non trivial square root of $1 \bmod x$. Trivial square root of 1 means 1 or -1 since $1^2 , -1^2 = 1$.

For example, $x = 1729$ and choose $z = 5$, and note that $x-1 = 1728 = 2^6 \times 27$

\[\begin{aligned} 5^{27} &\equiv 1217 \bmod 1729 \\ 5^{2\times27} &\equiv 1217 \equiv 1065 \bmod 1729 \\ 5^{2^2\times27} &\equiv 1065^2 \equiv 1 \bmod 1729 \\ 5^{2^2\times27} &\equiv 1^2 \equiv 1 \bmod 1729 \\ &\vdots \\ 5^{1728} &\equiv 1 \bmod 1729 \end{aligned}\]

So, when Fermat tests fail, we see if there is a non trivial square root of 1 exists.

It turns out that for a composite number $X$, even if its Carmichael, for at least three quarters of the choices of $Z$, this algorithm works.

This post is licensed under CC BY 4.0 by the author.