Gt Nlp M5

Posted May 16, 2024

By yxlow

8 min read

Document Semantics

Semantics: What word and phrase mean
Problem: Neural Networks don’t know what word means
- By extension neural network don’t know what a document is about
- Words are just one-hot vectors

So, How do we represent the meaning of a document?

Multi-hot
- Set a 1 in each position for every word in a document.
- The values are the same but some words are more important than others.
- If you want to figure out if two documents are related to each other you want to rely on words that are effective at distinguishing documents
- Look for ways to determine which words are important

Term Frequency-Inverse Document Frequency

TFIDF - a specific technique trying to decide whether two document are semantically similar to each other without really having the semantics of words and documents themselves.

Give weight to each word based on how important it is

Term frequency : If a word shows up frequently in a document, it must be more important than other words:

\[TF(w,d) = log(1+freq(w,d))\]

$freq(w,d)$ is how many times $w$ appears in document $d$
The log forces the TF to grow very slowly as the frequency of a word gets larger.

Inverse Document Frequency : Words that are common in all documents are not very important

\[IDF(w,D) = log \bigg( \frac{1 + \lvert D \lvert }{1 + count(w,D)}\bigg)+1\]

$ \lvert D \lvert$ is number of documents
$count(w,D)$ is how many documents in $D$ contains $w$
As the count increases, the ratio goes towards 1.

So, TF-IDF:

\[TFIDF(w,d,D) = TF(w,d) \times IDF(w,D)\]

Apply TF-IDF to every word $w$ in every document $d$ to get a vector

In summary:

TF-IDF provides a more nuanced document representation of a document than a multi-hot
Next we look at how to compute document similarity and retrieve the most similar documents

Measuring The Similarity Documents

Document Retrieval: given a word or a phrase (itself a document), compare the query to all other documents and return the most similar.
Given two documents, represented as vectors, how do we know how similar they are?

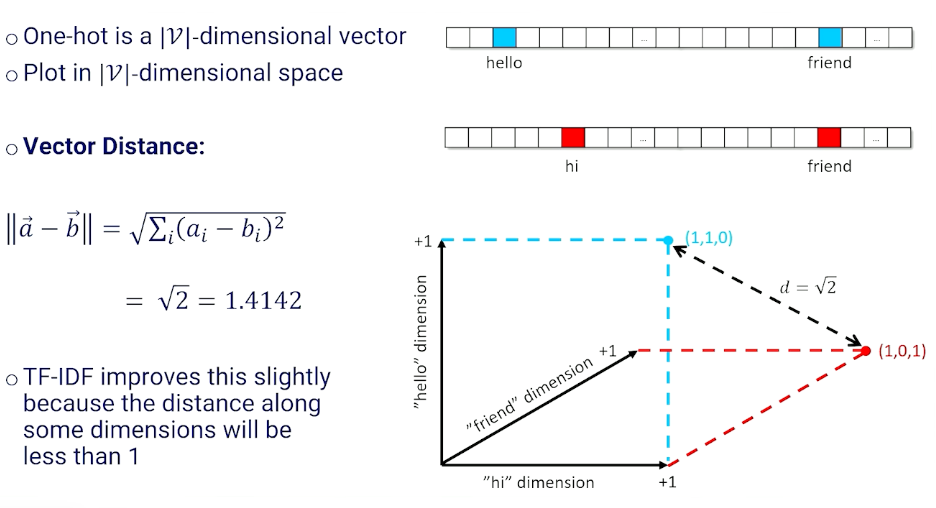
One way is to use the vector distance:

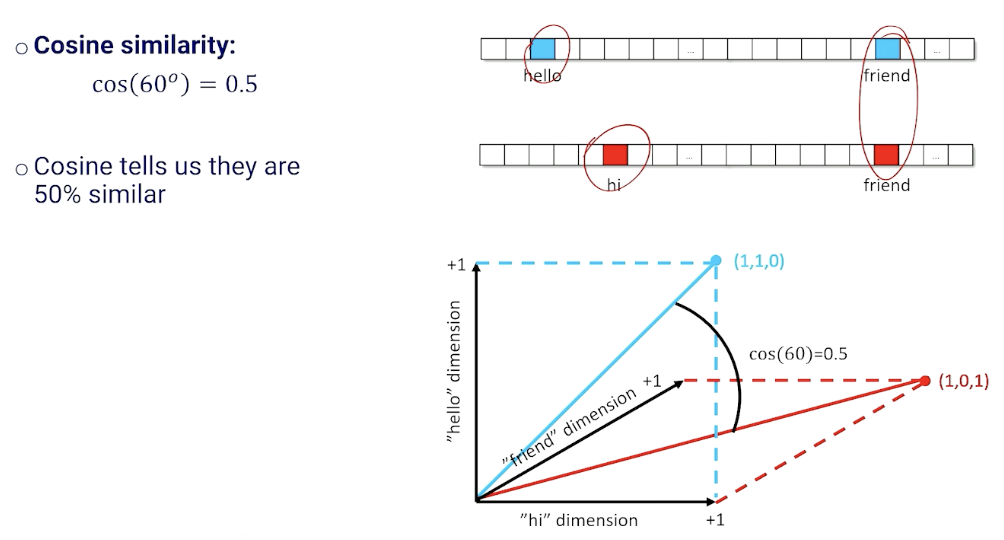
Another way is to use the cosine distance:

Now, on document retrieval:

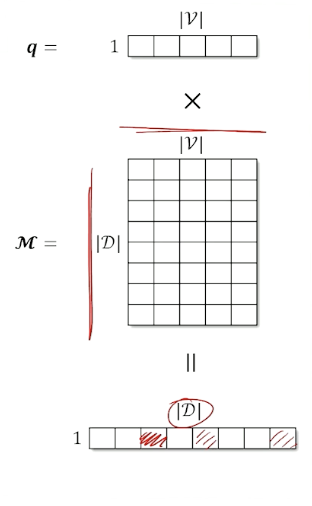
Create a $1 \times \lvert \mathcal{V} \lvert$ normalized documetn vector for the query($q$)
Create a normalized vector for every document and stack to create a $\lvert \mathcal{D} \lvert \times \lvert \mathcal{V} \lvert$ matrix $\mathcal{M}$.
Matrix multiply to get scores
Normalized the final vector
This is the same as computing the cosine similarity

\[cos(\vec{a},\vec{b}) = \frac{\vec{a} \cdot \vec{b}}{\lvert\lvert \vec{a}\lvert\lvert * \lvert\lvert\vec{b}\lvert\lvert}\]

Take the argmax to get the index of the document with the highest score (or get the top-k to return more than one)

There are still two issues:

Require a $\mathcal{V}$ length vector to represent a document
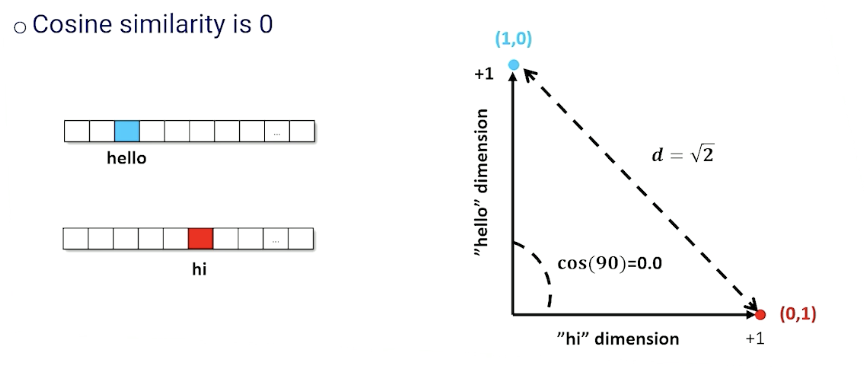
Does not capture the fact that some words are similar (“hi” vs “hello”)

Word Embeddings

The problem with TF-IDF just now is the way we index them in a vector even though they probably mean the same thing.

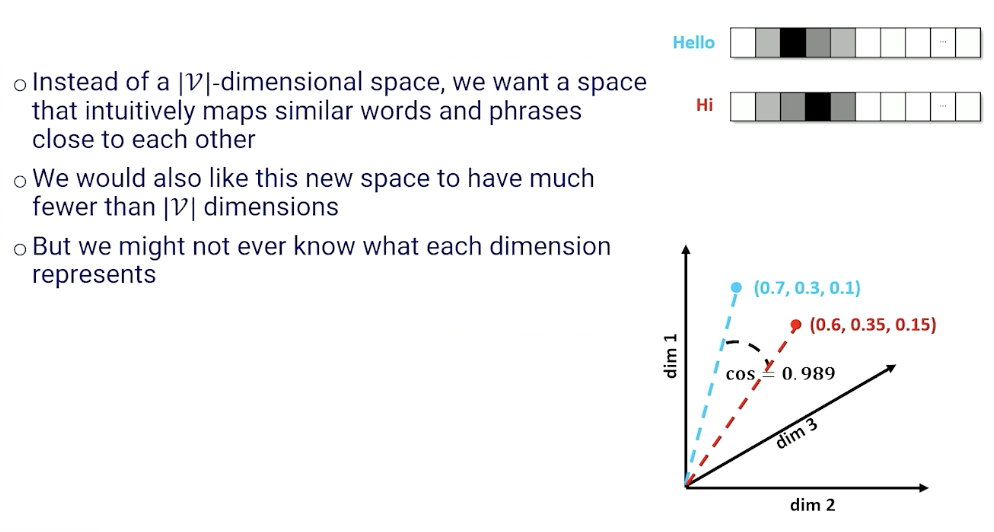
Instead of a $\lvert \mathcal{V} \lvert$ - dimensional space, we want a space that intuitively maps similar words and phrases close to each other. This is also known as embeddings:

So, how are we going to get these embeddings?

Take a one hot (or multi hot) and reduce it to a $d$ -dimensional space where $d \ll \lvert \mathcal{V} \lvert $
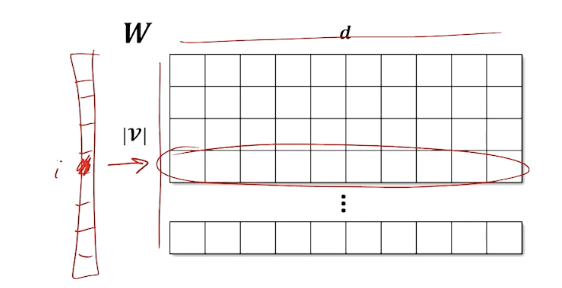
Use a linear layer with $\lvert \mathcal{V} \lvert \times d$ parameters $\mathcal{W}$
- Compress a one-hot into a d-dimensional vector

Why does this work?

One-hot for the $i^{th}$ word selects a set of $d$ weights and all others are zeroed out
These remaining weights are a $d$-dimensional representation of the indexed word
Because we are multiplying by 1s and 0s, the $d$ weights $W_i$ are identical to the $d$-dimensional vector of activations at the next layer up.

Looking at the matrix of weights in the linear layer:

Each row in $W$ is an embedding for each token in vocabulary
One-hot selects the row
Learn weights that capture whatever relationship we need

Word Embeddings Example

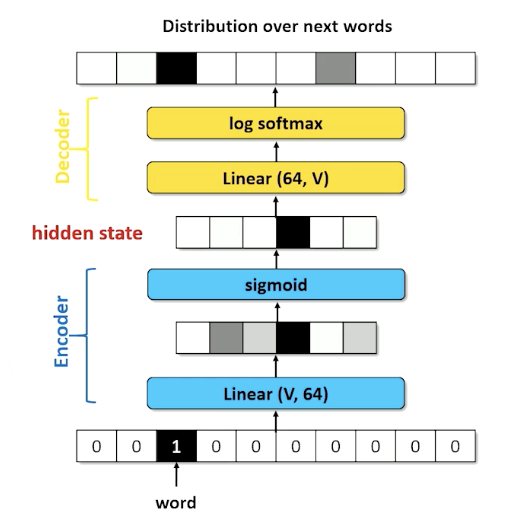
Recall the RNN architecture where we have an encoder layer:

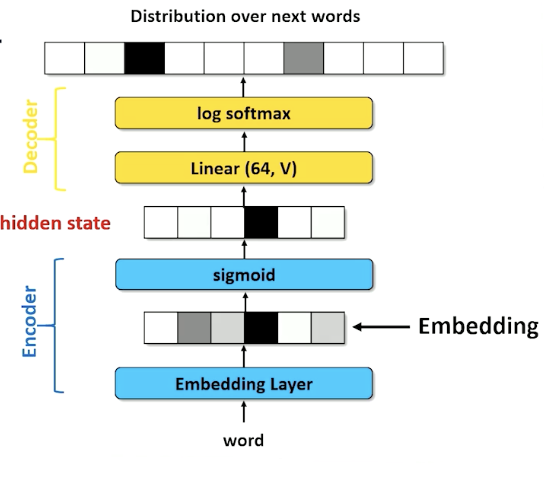
We call the lienar compression layer in the encoding the embedding layer:

token to one hot
Linear from length $\lvert \mathcal{V} \lvert$ to $d$ length vector
For simplicity moving forward, we are going to assume we can turn the word directly to an embedding.

Embedding layer in an RNN learns weights of an affine (linear) transformation
Whatever reduces loss in the output probability
- Must have compromises (words having similar activations)
- We hope those compromises map similar words to similar vectors
- Still no guarantee on semantic similarity
Embedding layer is task specific
- Because ultimately it is being fed into a NN with a loss function for a specific task.
Question: can we learn a general set of embedding?

Word2vec

Maybe we don’t need to know what each word means:

Distributional semantics : a word is known by by the company it keeps
Words that man approximately the same thing tend to be surrounded by the same word

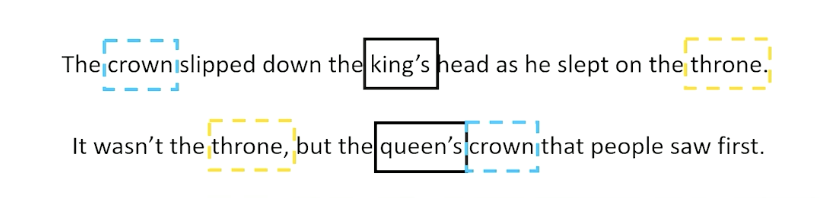
For example we always see king and queen together, maybe they mean something very similar in terms of semantics
Again - the idea is we don’t need to know what the word mean if words with similar meaning have similar embeddings

Then the question is:

How can we train an embedding to use this concept of distributional semantics
Can a word be predicted based on surrounding words?
- The crown was left on the throne when the ???? went to bed at night.
- Probably king or queen is a reasonable choice; although we can’t quite tell which is better
Can we predict the surrounding words based on a single word?

Take out a word in the middle of a sequence and ask a neural network to guess the missing word
Loss is the cross entropy of the probability distribution over words

Similarly, we can look at the opposite of the problem:

Can a window of words be predicted based on the word in the middle of the window?

Take a word and guess the words to the left and right
Loss is the cross entropy of each blank given the word in the middle
Break up into skip grams (bigram on non-adjacent tokens)
- E.g given word $w_t$, predict $w_{t-i}, w_{t+1}$ for some $i$.
Predict each skip-gram separately

This is also known as the word2vec approach and there are actually two approaches to word2vec:

continuous bag of words
or skip grams

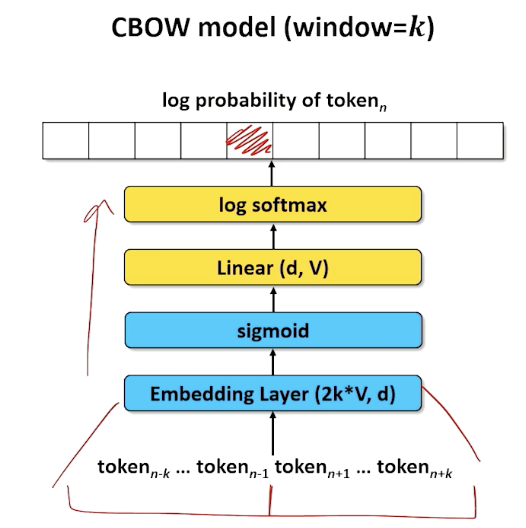
Let’s look at the continuous bag of words (known as CBOW) first, for a window of size $k$, what we are doing is we are taking a particular chunk of document and note that the document is missing a word in the middle.

So we take the $2k$ words off the left and right of the target word and asking the neural network to predict the missing word, in this case the embedding layer is $2k*V$ and outputs a/compresses it into $d$ dimension.

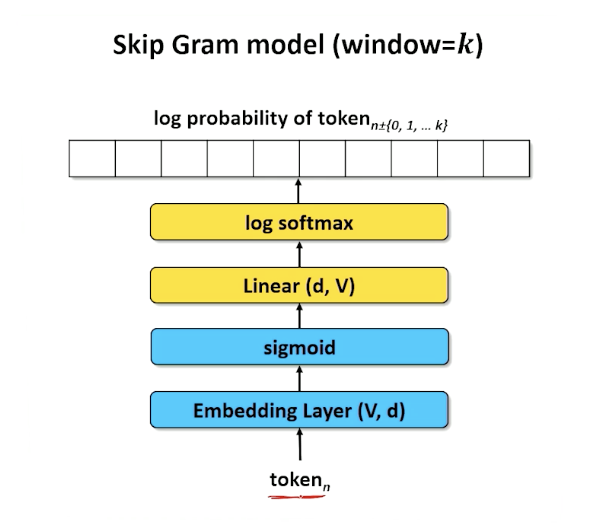
Now, let’s look at the skip gram model which is to look at a particular word and trying to guess the surrounding words

So again, the word will be turn into a dimension of size $d$
Because this is skip gram, we do not really care about the positions of the words but instead look at words with high activations.
- And the k highest activations are the words that are most likely to be in window around our $n^{th}$ word
- Doesn’t need to be a sentence, can be jumbled up - we are just looking for words
Compute the entropy of each of the prediction matches the actual words we would find in a span taken from our actual document.
- The math side of things is omitted which is a little complicated.

Embedding

Let’s see what we can do for our embeddings, remember in either CBOW or skip gram we have the embedding layer

We can extract teh weights from the embedding layer
- Each row is the embedding for a different token in the vocabulary

We can now do something interesting:

such as computing the cosine similarity using the embedding.
- $cos(\vec{v}{queen}, \vec{v})$
We can also do retrieval; find documents that are semantically similar
- Which Wikipedia document is most relevant to “Bank deposit”
  - Chattehoochee river
  - Great Recession of 2017
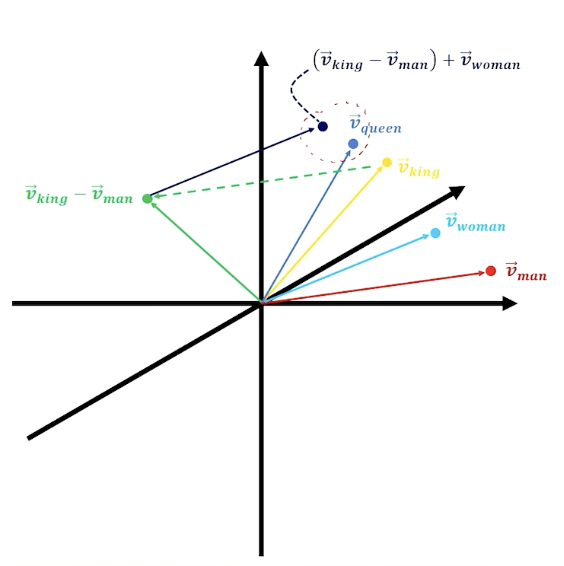
Can also do analogies - add and subtract word embeddings to compute analogies
- Georgia - California + peaches = ?

Again, to recap - words that represent similar concepts tend to be clustered closely in d-dimensional embedding space.

Vectors can be added and subtracted

E.g King - man + woman = Queen

Also:

Most points in embedding space are not words
Search for the nearest discrete point

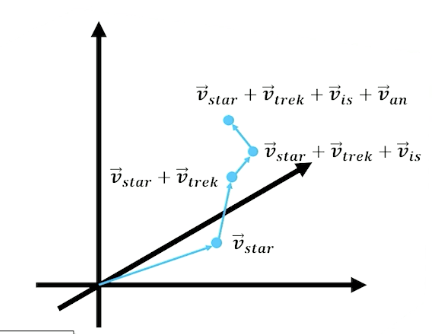
What about document embedding?

Add each word vector
Word vectors pointing in the same direction strengthen the semantic concept

Normalize the resultant vector
- Value of any of the $d$ dimension is the relative strength of that abstract semantic concept
- Necessary for cosine similarity